You are here: DAMASK>Documentation>Background>CrystalLattice>Hex







1.1.3. Hexagonal (hex)
Atom arrangement
Slip systems
| index | slip direction | plane normal |
| 1 | $[2 \bar 1 \bar 1 0]$ | $(0 0 0 1)$ |
| 2 | $[\bar 1 2 \bar 1 0]$ | $(0 0 0 1)$ |
| 3 | $[\bar 1 \bar 1 2 0]$ | $(0 0 0 1)$ |
 | ||
| Figure 3: Prismatic slip system in hexagonal lattice: $\langle 1 1 \bar 2 0\rangle \{1 0 \bar 1 0\}$ |
| index | slip direction | plane normal |
| 4 | $[2 \bar 1 \bar 1 0]$ | $(0 1 \bar 1 0)$ |
| 5 | $[\bar 1 2 \bar 1 0]$ | $(\bar 1 0 1 0)$ |
| 6 | $[\bar 1 \bar 1 2 0]$ | $(1 \bar 1 0 0)$ |
 | ||
| Figure 4: 2nd order prismatic compound slip system in hexagonal lattice: $\langle \bar 1 1 0 0\rangle \{1 1 \bar 2 0\}$ |
| index | slip direction | plane normal |
| 7 | $[0 1 \bar 1 0]$ | $(2 \bar 1 \bar 1 0)$ |
| 8 | $[\bar 1 0 1 0]$ | $(\bar 1 2 \bar 1 0)$ |
| 9 | $[1 \bar 1 0 0]$ | $(\bar 1 \bar 1 2 0)$ |
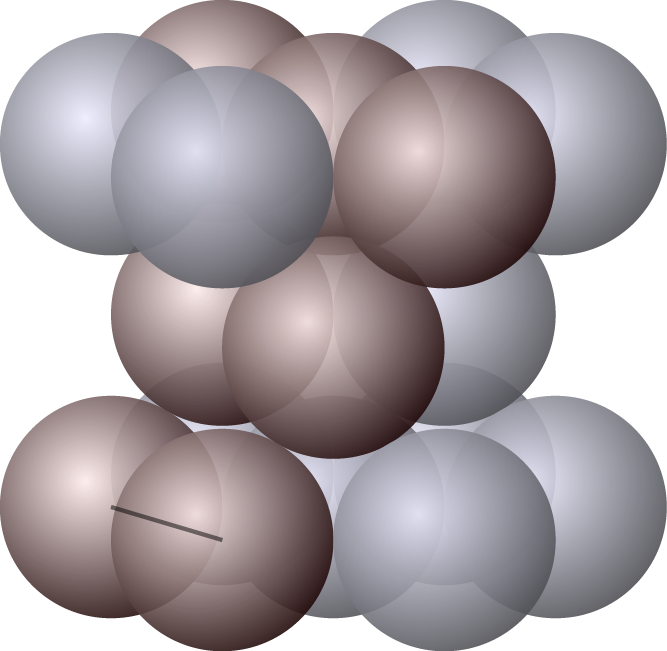 | ||
| Figure 5: 1st order pyramidal slip system in hexagonal lattice: $\langle 1 1 \bar 2 0\rangle \{1 0 \bar 1 1\}$ |
| index | slip direction | plane normal |
| 10 | $[2 \bar 1 \bar 1 0]$ | $(0 1 \bar 1 1)$ |
| 11 | $[\bar 1 2 \bar 1 0]$ | $(\bar 1 0 1 1)$ |
| 12 | $[\bar 1 \bar 1 2 0]$ | $(1 \bar 1 0 1)$ |
| 13 | $[1 1 \bar 2 0]$ | $(\bar 1 1 0 1)$ |
| 14 | $[\bar 2 1 1 0]$ | $(0 \bar 1 1 1)$ |
| 15 | $[1 \bar 2 1 0]$ | $(1 0 \bar 1 1)$ |
 | ||
| Figure 6: 1st order pyramidal <c+a> slip system in hexagonal lattice: $\langle 1 1 \bar 2 3\rangle \{1 0 \bar 1 1\}$ |
| index | slip direction | plane normal |
| 16 | $[2 \bar 1 \bar 1 3]$ | $(\bar 1 1 0 1)$ |
| 17 | $[1 \bar 2 1 3]$ | $(\bar 1 1 0 1)$ |
| 18 | $[\bar 1 \bar 1 2 3]$ | $(1 0 \bar 1 1)$ |
| 19 | $[\bar 2 1 1 3]$ | $(1 0 \bar 1 1)$ |
| 20 | $[\bar 1 2 \bar 1 3]$ | $(0 \bar 1 1 1)$ |
| 21 | $[1 1 \bar 2 3]$ | $(0 \bar 1 1 1)$ |
| 22 | $[\bar 2 1 1 3]$ | $(1 \bar 1 0 1)$ |
| 23 | $[\bar 1 2 \bar 1 3]$ | $(1 \bar 1 0 1)$ |
| 24 | $[1 1 \bar 2 3]$ | $(\bar 1 0 1 1)$ |
| 25 | $[2 \bar 1 \bar 1 3]$ | $(\bar 1 0 1 1)$ |
| 26 | $[1 \bar 2 1 3]$ | $(0 1 \bar 1 1)$ |
| 27 | $[\bar 1 \bar 1 2 3]$ | $(0 1 \bar 1 1)$ |
 | ||
| Figure 7: 2nd order pyramidal <c+a> slip system in hexagonal lattice: $\langle 1 1 \bar 2 3\rangle \{1 1 \bar 2 2\}$ |
| index | slip direction | plane normal |
| 28 | $[2 \bar 1 \bar 1 3]$ | $(\bar 2 1 1 2)$ |
| 29 | $[\bar 1 2 \bar 1 3]$ | $(1 \bar 2 1 2)$ |
| 30 | $[\bar 1 \bar 1 2 3]$ | $(1 1 \bar 2 2)$ |
| 31 | $[\bar 2 1 1 3]$ | $(2 \bar 1 \bar 1 2)$ |
| 32 | $[1 \bar 2 1 3]$ | $(\bar 1 2 \bar 1 2)$ |
| 33 | $[1 1 \bar 2 3]$ | $(\bar 1 \bar 1 2 2)$ |
Twin systems
.png) | ||
| Figure 8: $K_1$ $\langle 1 0 \bar 1 \bar 1\rangle$ - $n_1$ $\{1 0 \bar 1 2\}$ T1 - Tensile twinning in Co, Mg, Zr, Ti, and Be; compressive twinning in Cd and Zn. |
| $\eta_1$ | $K_1$ | $\eta_2$ | $K_2$ |
| $\langle \bar 1 0 1 1\rangle$ | $\{1 0 \bar 1 2\}$ | $\langle 1 0 \bar 1 1\rangle$ | $\{1 0 \bar 1 \bar 2\}$ |
| index | slip direction | plane normal |
| 1 | $[1 \bar 1 0 1]$ | $(\bar 1 1 0 2)$ |
| 2 | $[\bar 1 0 1 1]$ | $(1 0 \bar 1 2)$ |
| 3 | $[0 1 \bar 1 1]$ | $(0 \bar 1 1 2)$ |
| 4 | $[\bar 1 1 0 1]$ | $(1 \bar 1 0 2)$ |
| 5 | $[1 0 \bar 1 1]$ | $(\bar 1 0 1 2)$ |
| 6 | $[0 \bar 1 1 1]$ | $(0 1 \bar 1 2)$ |
.png) | ||
| Figure 9: $K_1$ $\langle \bar 1 \bar 1 2 6\rangle$ - $n_1$ $\{1 1 \bar 2 1\}$ T2 - Tensile twinning in Co, Re, and Zr. |
| $\eta_1$ | $K_1$ | $\eta_2$ | $K_2$ |
| $\langle \bar 1 \bar 1 2 6\rangle$ | $\{1 1 \bar 2 1\}$ | $\langle 1 1 2 0\rangle$ | $\{0 0 0 2\}$ |
| index | slip direction | plane normal |
| 7 | $[2 \bar 1 \bar 1 6]$ | $(\bar 2 1 1 1)$ |
| 8 | $[\bar 1 2 \bar 1 6]$ | $(1 \bar 2 1 1)$ |
| 9 | $[\bar 1 \bar 1 2 6]$ | $(1 1 \bar 2 1)$ |
| 10 | $[\bar 2 1 1 6]$ | $(2 \bar 1 \bar 1 1)$ |
| 11 | $[1 \bar 2 1 6]$ | $(\bar 1 2 \bar 1 1)$ |
| 12 | $[1 1 \bar 2 6]$ | $(\bar 1 \bar 1 2 1)$ |
.png) | ||
| Figure 10: $K_1$ $\langle 1 0 \bar 1 \bar 2\rangle$ - $n_1$ $\{1 0 \bar 1 1\}$ C1 - Compressive twinning in Mg. |
| $\eta_1$ | $K_1$ | $\eta_2$ | $K_2$ |
| $\langle 1 0 \bar 1 \bar 2\rangle$ | $\{1 0 \bar 1 1\}$ | $\langle 3 0 \bar 3 2\rangle$ | $\{1 0 \bar 1 \bar 3\}$ |
| index | slip direction | plane normal |
| 13 | $[\bar 1 1 0 \bar 2]$ | $(\bar 1 1 0 1)$ |
| 14 | $[1 0 \bar 1 \bar 2]$ | $(1 0 \bar 1 1)$ |
| 15 | $[0 \bar 1 1 \bar 2]$ | $(0 \bar 1 1 1)$ |
| 16 | $[1 \bar 1 0 \bar 2]$ | $(1 \bar 1 0 1)$ |
| 17 | $[\bar 1 0 1 \bar 2]$ | $(\bar 1 0 1 1)$ |
| 18 | $[0 1 \bar 1 \bar 2]$ | $(0 1 \bar 1 1)$ |
.png) | ||
| Figure 11: $K_1$ $\langle 1 1 \bar 2 \bar 3\rangle$ - $n_1$ $\{1 1 \bar 2 2\}$ C2 - Compressive twinning in Ti and Zr. |
| $\eta_1$ | $K_1$ | $\eta_2$ | $K_2$ |
| $\langle 1 1 \bar 2 \bar 3\rangle$ | $\{1 1 \bar 2 2\}$ | $\langle 2 2 \bar 4 3\rangle$ | $\{1 1 \bar 2 \bar 4\}$ |
| index | slip direction | plane normal |
| 19 | $[2 \bar 1 \bar 1 \bar 3]$ | $(2 \bar 1 \bar 1 2)$ |
| 20 | $[\bar 1 2 \bar 1 \bar 3]$ | $(\bar 1 2 \bar 1 2)$ |
| 21 | $[\bar 1 \bar 1 2 \bar 3]$ | $(\bar 1 \bar 1 2 2)$ |
| 22 | $[\bar 2 1 1 \bar 3]$ | $(\bar 2 1 1 2)$ |
| 23 | $[1 \bar 2 1 \bar 3]$ | $(1 \bar 2 1 2)$ |
| 24 | $[1 1 \bar 2 \bar 3]$ | $(1 1 \bar 2 2)$ |
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
0_Indexation_topview.svg | manage | 456 bytes | 23 May 2013 - 09:34 | DavidMercier | Indexation of the hexagonal unit cell |
| |
HCP_crystal_structure.png | manage | 168 K | 17 Oct 2012 - 17:21 | PhilipEisenlohr | Hexagonal lattice structure |
| |
HCP_crystal_structure.svg | manage | 2 K | 17 Oct 2012 - 17:20 | PhilipEisenlohr | Hexagonal lattice structure (vector-based) |
| |
HCP_slip_system_basal.png | manage | 175 K | 17 Oct 2012 - 17:29 | PhilipEisenlohr | Hexagonal slip system basal |
| |
HCP_slip_system_basal.svg | manage | 3 K | 17 Oct 2012 - 17:29 | PhilipEisenlohr | Hexagonal slip system basal (vector-based) |
| |
HCP_slip_system_prism2nd_a.png | manage | 194 K | 25 Jun 2013 - 10:33 | DavidMercier | Hexagonal slip system 2nd prismatic [a] |
| |
HCP_slip_system_prism2nd_a.svg | manage | 3 K | 25 Jun 2013 - 10:33 | DavidMercier | Hexagonal slip system 2nd prismatic [a] (vector based) |
| |
HCP_slip_system_prism_a.png | manage | 189 K | 17 Oct 2012 - 17:40 | PhilipEisenlohr | Hexagonal slip system prismatic [a] |
| |
HCP_slip_system_prism_a.svg | manage | 3 K | 17 Oct 2012 - 17:39 | PhilipEisenlohr | Hexagonal slip system prismatic [a] (vector-based) |
| |
HCP_slip_system_pyramidal1st_a.png | manage | 199 K | 17 Oct 2012 - 20:28 | PhilipEisenlohr | Hexagonal slip system 1st pyramidal [a] |
| |
HCP_slip_system_pyramidal1st_a.svg | manage | 3 K | 17 Oct 2012 - 20:27 | PhilipEisenlohr | Hexagonal slip system 1st pyramidal [a] (vector-based) |
| |
HCP_slip_system_pyramidal1st_c+a.png | manage | 203 K | 17 Oct 2012 - 20:19 | PhilipEisenlohr | Hexagonal slip system 1st pyramidal [c+a] |
| |
HCP_slip_system_pyramidal1st_c+a.svg | manage | 3 K | 17 Oct 2012 - 20:19 | PhilipEisenlohr | Hexagonal slip system 1st pyramidal [c+a] (vector-based) |
| |
HCP_slip_system_pyramidal2nd_c+a.png | manage | 196 K | 17 Oct 2012 - 20:46 | PhilipEisenlohr | Hexagonal slip system 2nd pyramidal [c+a] |
| |
HCP_slip_system_pyramidal2nd_c+a.svg | manage | 3 K | 17 Oct 2012 - 20:46 | PhilipEisenlohr | Hexagonal slip system 2nd pyramidal [c+a] (vector-based) |
| |
HCP_twin_system_compressive_K1(10-11).png | manage | 197 K | 23 May 2013 - 09:59 | DavidMercier | Hexagonal twin system compressive K1(10-11) |
| |
HCP_twin_system_compressive_K1(10-11).svg | manage | 3 K | 23 May 2013 - 10:00 | DavidMercier | Hexagonal twin system compressive K1(10-11) (vector based) |
| |
HCP_twin_system_compressive_K1(11-22).png | manage | 196 K | 23 May 2013 - 10:02 | DavidMercier | Hexagonal twin system compressive K1(11-22) |
| |
HCP_twin_system_compressive_K1(11-22).svg | manage | 3 K | 23 May 2013 - 10:03 | DavidMercier | Hexagonal twin system compressive K1(11-22) (vector based) |
| |
HCP_twin_system_tensile_K1(-1012).png | manage | 193 K | 23 May 2013 - 12:16 | DavidMercier | Hexagonal twin system tensile K1(-1012) |
| |
HCP_twin_system_tensile_K1(-1012).svg | manage | 3 K | 23 May 2013 - 12:16 | DavidMercier | Hexagonal twin system tensile K1(-1012) (vector-based) |
| |
HCP_twin_system_tensile_K1(11-21).png | manage | 226 K | 23 May 2013 - 11:53 | DavidMercier | Hexagonal twin system tensile K1(11-21) |
| |
HCP_twin_system_tensile_K1(11-21).svg | manage | 3 K | 23 May 2013 - 11:53 | DavidMercier | Hexagonal twin system tensile K1(11-21) (vector-based) |
Edit | Attach | Print version | History: r29 < r28 < r27 < r26 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r29 - 12 Feb 2019, PhilipEisenlohr
- News
- 14 Sep 2020
-
CMCn2020 & DAMASK user meeting to be hosted at Max-Planck-Institut für Eisenforschung(cancelled) - 22 Aug 2020
- Release of first preview version of DAMASK 3
- 19 Feb 2020
- DAMASK made it to the Advanved Engineering Materials Hall of Fame
- 26 Mar 2019
- DREAM.3D 6.5.119
(released 2019/03/22) comes with a DAMASK export filter - 25 Mar 2019
- Release of version v2.0.3
- 21 Jan 2019
- DAMASK overview paper finally published with full citation information available
- 01 Dec 2018
- DAMASK overview paper now online
- 17 Sep 2018
- CMCn2018 & DAMASK user meeting to be hosted at Max-Planck-Institut für Eisenforschung
- 22 May 2018
- Release of version v2.0.2
- 01 Sep 2016
- CMCn2016 & DAMASK user meeting to be hosted at Max-Planck-Institut für Eisenforschung
- 25 Jul 2016
- Release of version v2.0.1
- 08 Mar 2016
- Release of version v2.0.0
- 22 Feb 2016
- New webserver up and running
- 09 Feb 2016
- Migrated code repository from Subversion to GitLab
- 17 Dec 2014
- Release of revision 3813
- 14 May 2014
- Release of revision 3108
- 02 Apr 2014
- Release of revision 3062
- 16 Oct 2013
- Release of revision 2689
- 15 Jul 2013
- Release of revision 2555
- 15 Feb 2013
- Release of revision 2174
- 13 Feb 2013
-
 documentation
documentation
- 16 Dec 2012
-
 rendering
rendering
- 23 Nov 2012
- Release of revision 1955
- 15 Nov 2012
- Release of revision 1924
- 01 Nov 2012
- Updated sidebar
- 30 Oct 2012
- Significant website updates and content extensions
Ideas, requests, problems regarding DAMASK? Send feedback
§ Imprint § Data Protection


